Precise Lose Between Float64 and Uint64¶

In astjson library, the lexer scans the number and stores the respective bytes. Then the parser will parse the bytes to number which is expressed by a float64. It works well at beginning, however, once I added a corner case of number with value math.MaxUint64(1<<64 - 1 or decimal value 18446744073709551615), the parser cannot work as expected. It's indeed a bug issue.

The simplified problem is the value through debug of f is 18446744073709552000 instead of 18446744073709551615.

f, _ = strconv.ParseFloat("18446744073709551615", 64)

The unexpected behavior thwarts the accurate of astjson, hence I investigate and write the document for further reference.

It's the issue that the conversion between float64 and uint64 has some implications which contravenes the ordinary ideas about type cast. As a result, diving further into the very basic definition is crucial to learn about this issue.

Float and IEEE754¶

IEEE754 talks about the real world practice about float and double number. In this topic, we talk about the double(64 bit float number) only.

The layout of a float64 is shown below:

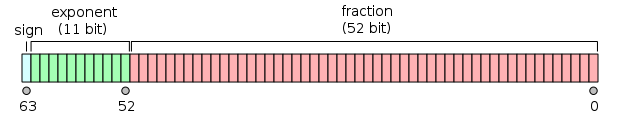
The IEEE 754 standard specifies a binary64 as having:

• Sign bit: 1 bit
• Exponent: 11 bits
• Significand precision: 53 bits (52 explicitly stored)

The real value by a given 64-bit double-precision datum with a given biased exponent is calculated by this fomulation:

For example, the float64 number below represents the number of 18446744073709551616. It will be calculated with the following steps:

Round to Nearest Even¶

When conversion from uint64 to float64, the go compiler rounds halt to even. By this convention, if the fractional part of x is 0.5, then y is the even integer nearest to x. Thus, for example, 23.5 becomes 24, as does 24.5; however, −23.5 becomes −24, as does −24.5. This function minimizes the expected error when summing over rounded figures, even when the inputs are mostly positive or mostly negative, provided they are neither mostly even nor mostly odd.

Some examples for 32-bits float number:

+----------------+----------------+--------------+----------------------+
| Input(integer) | After Rounding | Precise Lose | Float Hex in IEEE754 |
+----------------+----------------+--------------+----------------------+
| 100            | 100            | 0            | 0x42c80000           |
+----------------+----------------+--------------+----------------------+
| 77889900       | 77889904       | 4            | 0x4c94902e           |
+----------------+----------------+--------------+----------------------+
| 123456789      | 123456792      | 3            | 0x4ceb79a3           |
+----------------+----------------+--------------+----------------------+

In go, when you var f float32=77889900, the f will be rounded by runtime.

// f is rounded after assignment
var f float32=77889900
// the output will be 77889904
fmt.Println(uint32(f))

Overflow Outputs Vary in Different CPU Platforms¶

Because the number is overflow after rounding, the outputs of the below code snippet vary among CPU platforms.

func main() {
    var u uint64 = 18446744073709551615
    f := float64(u)
    fmt.Println(f)
    fmt.Println(uint64(f))
}

+-----------------+------------------------+------------------------+
|                 | ARM                    | Intel                  |
+-----------------+------------------------+------------------------+
| Float           | 1.8446744073709552e+19 | 1.8446744073709552e+19 |
| Expression      |                        |                        |
+-----------------+------------------------+------------------------+
| Decimal Value   | 18446744073709551615   | 9223372036854775808    |
+-----------------+------------------------+------------------------+
| Binary Format   | 0xFFFFFFFFFFFFFFFF     | 0x8000000000000000     |
| (no signed bit) |                        |                        |
+-----------------+------------------------+------------------------+

Overflow and Conversion¶

The CPU result vary because the logic of handling overflow. The CPU converts the float value and get the precise underlying value, then use an unsigned integer format to express it. However, because it's overflow(\(2^{64}\)) which is larger than max unsigned integer 64), CPU cast it differently.

When CPU converts float to an unsigned integer, it will firstly create a 64-bits place to hold it in a registeri(eg, RAX). Then, it will start to calculate the integer values of a IEEE-754 float number.

• ARM:
  After calculating \(2^{63}\)(1 << 63), ARM will left shift the number. However, it finds an overflow error and then put all bits to one, which means when overflowing, it just discards the overflow parts and express the largest number within its limitation(\(2^{64}-1\)).

• Intel: I don't have much idea about the output on intel.

Convertion Functions in Go Language¶

Go language provides math, strconv and native type conversion. Here I left some epherical cases:

+----------------------+---------------------+---------------------+----------------------------+
| Input and Expected   | math.Float64bits    | uint                | strconv.ParseUint          |
+----------------------+---------------------+---------------------+----------------------------+
| 2                    | 4611686018427387904 | 2                   | 2 <nil>                    |
+----------------------+---------------------+---------------------+----------------------------+
| 9223372036854775808  | 4890909195324358656 | 9223372036854775808 | 9223372036854775808 <nil>  |
+----------------------+---------------------+---------------------+----------------------------+
| 18446744073709551615 | 4895412794951729152 | 9223372036854775808 | 18446744073709551615, nil  |
+----------------------+---------------------+---------------------+----------------------------+
| 18446744073709551616 | 4895412794951729152 | 9223372036854775808 | 18446744073709551615,      |
|                      |                     |                     | strconv.ParseUint:parsing  |
|                      |                     |                     | "18446744073709551616":    |
|                      |                     |                     | value out of range         |
+----------------------+---------------------+---------------------+----------------------------+

package main

import (
    "fmt"
    "math"
    "strconv"
)

func main() {
    f := float64(2)
    fmt.Println(math.Float64bits(f))
    fmt.Println(uint64(f))
    fmt.Println(strconv.ParseUint("2", 10, 64))

    f = float64(9223372036854775808)
    fmt.Println(math.Float64bits(f))
    fmt.Println(uint64(f))
    fmt.Println(strconv.ParseUint("9223372036854775808", 10, 64))

    f = float64(18446744073709551615)
    fmt.Println(math.Float64bits(f))
    fmt.Println(uint64(f))
    fmt.Println(strconv.ParseUint("18446744073709551615", 10, 64))

    f = float64(18446744073709551616)
    fmt.Println(math.Float64bits(f))
    fmt.Println(uint64(f))
    fmt.Println(strconv.ParseUint("18446744073709551616", 10, 64))
}

The conclusions are:

Float64Bits for IEEE expression¶

Use math.Float64bits to see a float64 IEEE expression.

    f, _ = strconv.ParseFloat("18446744073709551615", 64)
    str := strconv.FormatUint(math.Float64bits(f), 2)
    // output: 100001111110000000000000000000000000000000000000000000000000000 63
    fmt.Println(str, len(str))

strconv.ParseUint for reporting overflow¶

Use strconv.ParseUint could report overflow:

    ui, err := strconv.ParseUint("18446744073709551616", 10, 64)
    // 18446744073709551615 strconv.ParseUint: parsing "18446744073709551616": value out of range
    fmt.Println(ui, err)

uint64() for casting float to uint¶

Use uint64() to convert float to uint, but uint64 cannot avoid the losing precise during rounding.

How Go Math Library Knows the Platform Bits?¶

In src/math/const.go, there is a constant intSize:

const (
    intSize = 32 << (^uint(0) >> 63)
)